PhD (Defense Passed) RECORDING Michigan State University blankjul [at] msu.edu
Julian Blank is a Ph.D. candidate at the Department of Computer Science and Engineering at Michigan State University. He received his B.Sc. in Business Information Systems from Otto von Guericke University, Germany, in 2010. He was a visiting scholar at the Michigan State University, Michigan, USA in 2015, and finished his M.Sc. in Computer Science at Otto von Guericke University, Germany, in 2016. He is the leading developer of pymoo, an open-source multi-objective optimization framework in Python. His research interests include evolutionary computation, multi-objective optimization, surrogate-assisted optimization, and machine learning.
CV / Biography / Google Scholar / Research Gate LinkedIn / Xing / Github
Research
Julian Blank, Kalyanmoy Deb
Springer, Memetic Computing, 2021. Submitted.
The performance assessment of the objective and constraints often requires running different software packages separately along with evaluating mathematically defined functions with significantly different (heterogeneous) computing times. A single software package may compute a functional group of objectives and constraints as a block, thereby creating a complicated computing pattern in evaluating a single population member. While much effort has been made to handle computationally expensive functions in the literature, little attention has been paid to handle heterogeneously expensive optimization problems. This paper focuses on efficient and adaptive ways to schedule an evaluation of different functional groups of objectives and constraints by utilizing the potential of offspring population members in terms of their multi-objective ranks, the accuracy of low-fidelity models to predict their function values, and their computing times.
source code
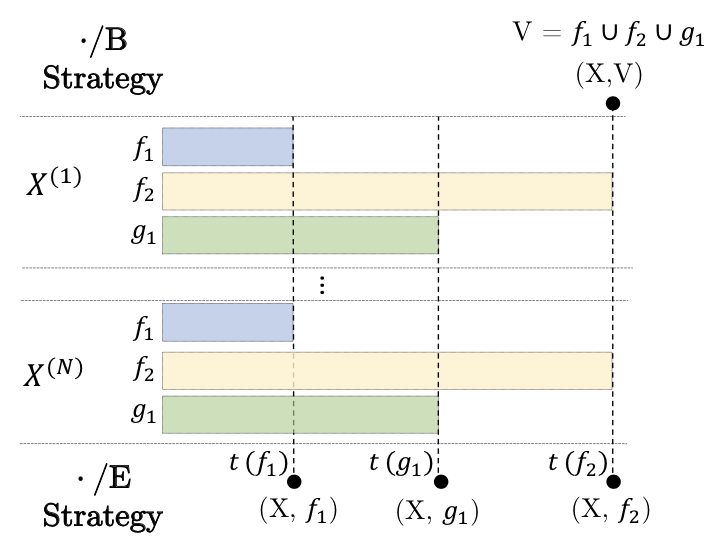
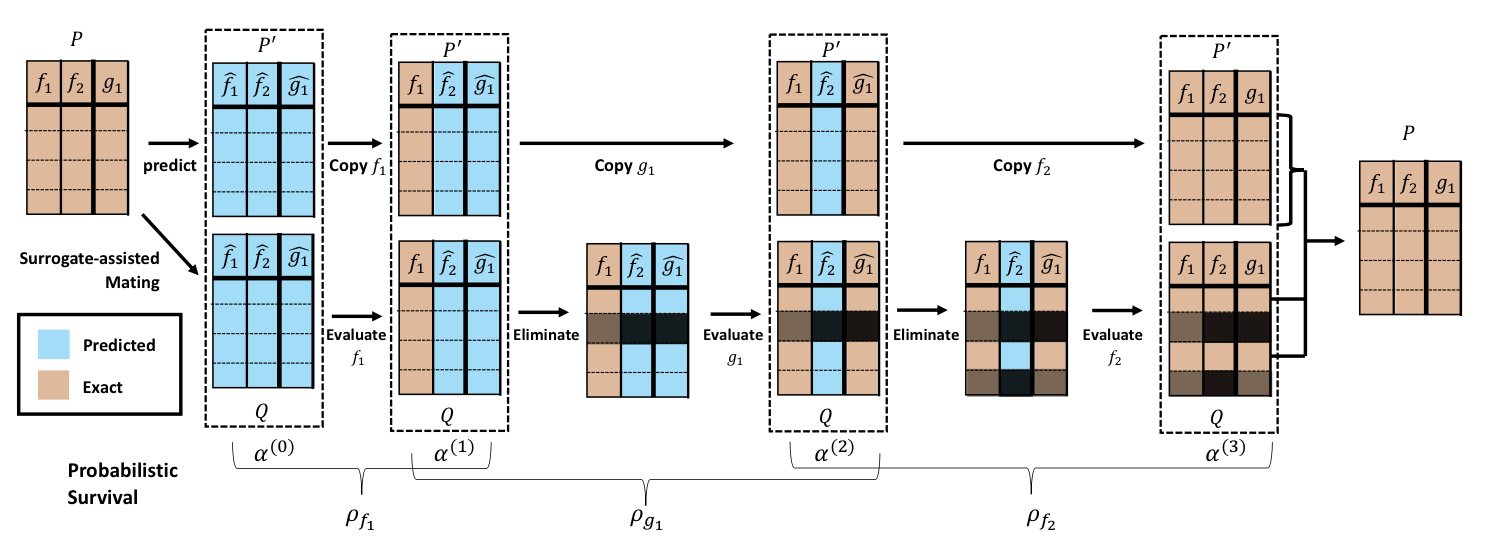
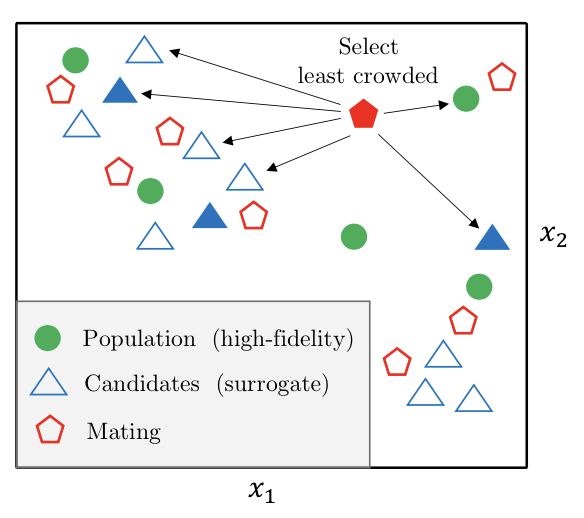
Julian Blank, Kalyanmoy Deb
GECCO, 2021.
This paper proposes a probabilistic surrogate-assisted framework (PSAF), demonstrating its applicability to a broad category of single-objective optimization methods. The framework injects knowledge from a surrogate into an existing algorithm through a tournament-based procedure and continuing the optimization run on the surrogate's predictions. The surrogate's involvement is determined by updating a replacement probability based on the accuracy from past iterations. A study of four well-known population-based optimization algorithms with and without the proposed probabilistic surrogate assistance indicates its usefulness in achieving a better convergence.
link / pdf / bibtex
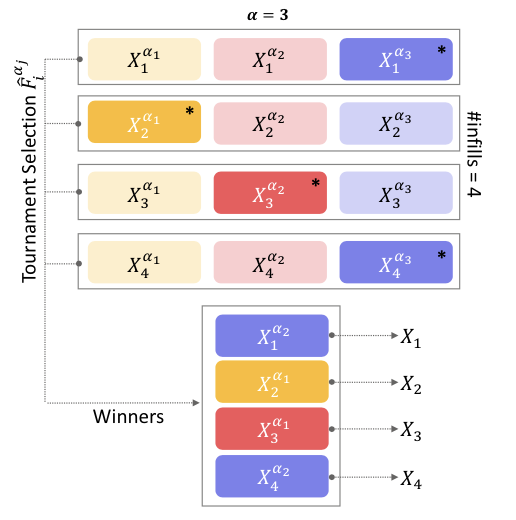
Julian Blank, Kalyanmoy Deb
EMO, 2021.
Constraints have often been neglected or assumed to be a by-product of computationally expensive objective computation. Many optimization problems in practice have computationally inexpensive geometrical or physical constraint functions, while the objectives may still be computationally expensive. This scenario probably makes the simplest case of handling heterogeneous and multi-scale surrogate modeling in the presence of constraints. In this paper, we propose a method which makes use of the inexpensiveness of constraints to ensure all time-consuming objective evaluations are only executed for feasible solutions.
link / pdf / slides / source code / bibtex
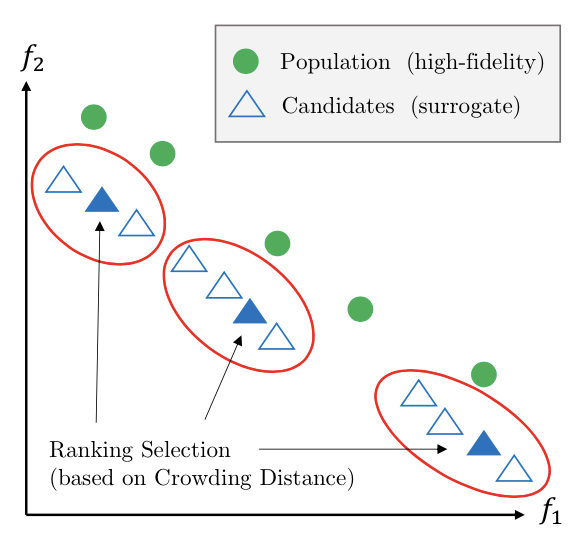
Julian Blank, Kalyanmoy Deb
IMCIC, 2021.
Collaboration among different stakeholders in achieving a problem-solving task is increasingly recognized as a vital component of applied research today. While many articles on the outcome of such collaborations have been published, and the justification of domain-specific information within an optimization has been established, systematic approaches to collaborative optimization have not been proposed yet. In this paper, methodical descriptions and challenges of collaborative optimization in practice are provided, and a blueprint illustrating the essential phases of the collaborative process is proposed. Moreover, collaborative optimization is illustrated by case studies of previous optimization projects with several industries. The study should encourage and pave the way for optimization researchers and practitioners to come together and embrace each other's expertise to solve complex problems of the twenty-first century.
pdf / bibtex
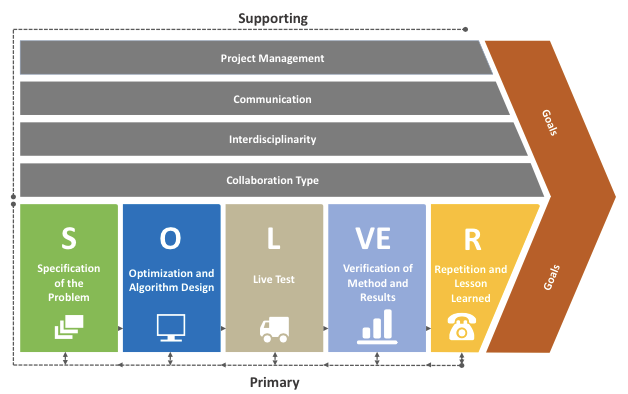
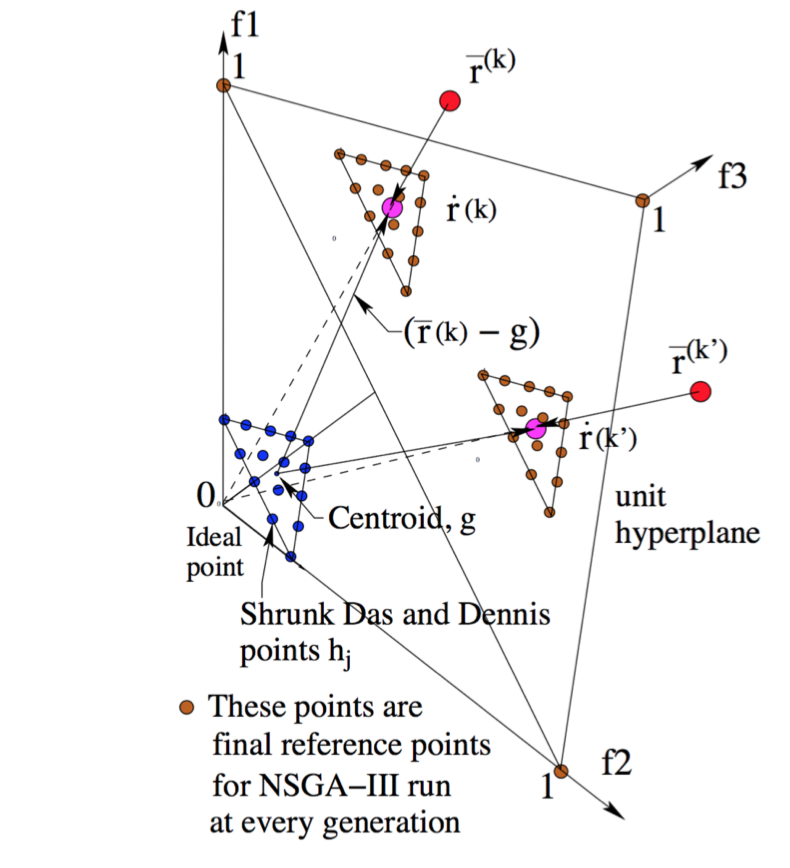
Julian Blank, Kalyanmoy Deb, Yashesh Dhebar, Sunith Bandaru, Haitham Seada
IEEE Transactions on Evolutionary Computation (TEVC), 2020.
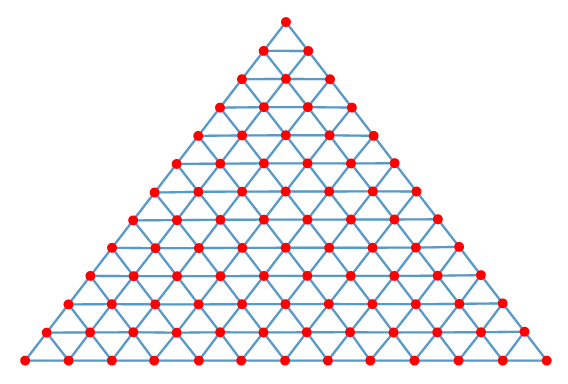
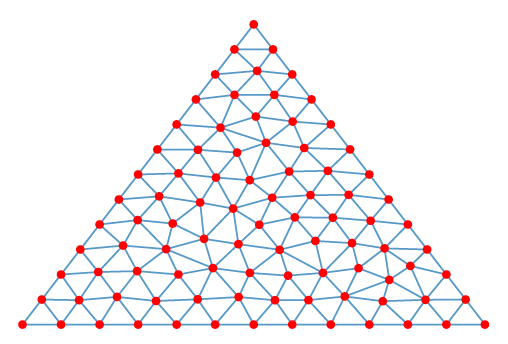
A generic procedure to distribute a set of points of arbitrary size well-spaced on a unit simplex. The resulting point set is commonly used as references directions for many-objective optimization problems and EMO researchers always felt the need for a more generic approach. We show that an iterative improvement based on Riesz s-Energy is able to effectively find an arbitrary number of well-spaced points even in higher-dimensional spaces.
link / data / source code / bibtex
Julian Blank, Kalyanmoy Deb
IEEE World Congress on Computational Intelligence (WCCI), 2020.
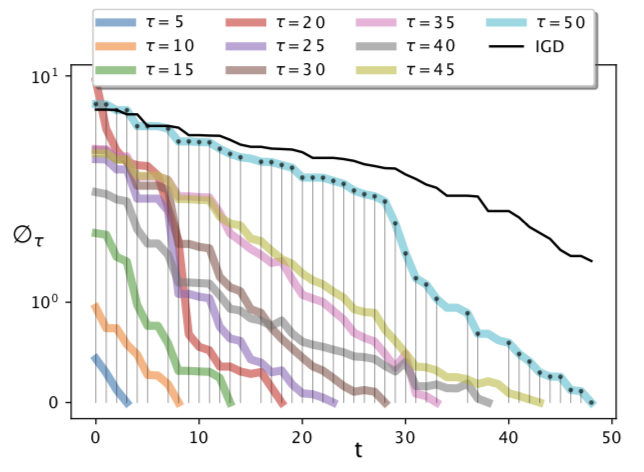
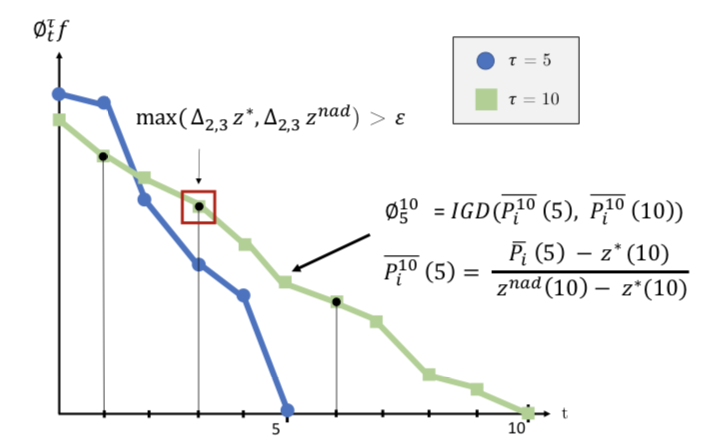
Most performance metrics assume that the knowledge of the exact Pareto-optimal set is available. In this paper, we investigate a running performance metric which can be applied to measure the performance at any time during the algorithm execution and no true optimum needs to be known for computing the metric. Moreover, by introducing a threshold and comparing the values of indicators a set of termination criteria is also suggested.
link / pdf / source code / bibtex
Ali Ahrari, Julian Blank Kalyanmoy Deb, Xianren Li
Engineering Optimization, 2020.
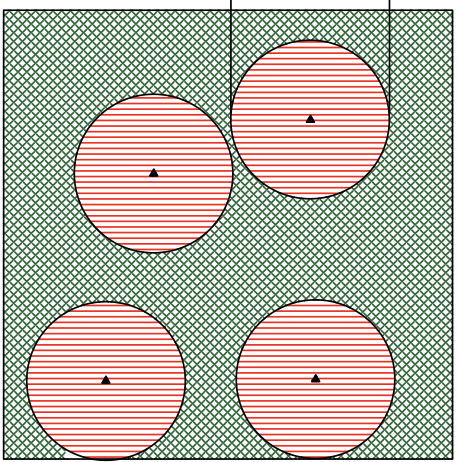
Many engineering design problems are associated with computationally expensive simulations for design evaluation, which makes the optimization process a time-consuming effort which requires each candidate design to be selected carefully. This study develops a niching-based surrogate-assisted evolutionary algorithm which uses a trust-region concept to control the evaluation error. At the same time, maximizing the information about specific regions of the search space is pursued by proper selection of new candidate solutions.
link / pdf / bibtex

Julian Blank and Kalyanmoy Deb
IEEE Access, 2020.
We have developed pymoo, a multi-objective optimization framework in Python. We provide a guide to getting started with our framework by demonstrating the implementation of an exemplary constrained multi-objective optimization scenario. Moreover, we give a high-level overview of the architecture of pymoo to show its capabilities followed by an explanation of each module and its corresponding sub-modules. The implementations in our framework are customizable and algorithms can be modified/extended by supplying custom operators.
link / pdf / documentation / bibtex

Philipp Back, Antti Suominen, Pekka Malo, Olli Tahvonen, Julian Blank, Kalyanmoy Deb
GECCO, 2020.
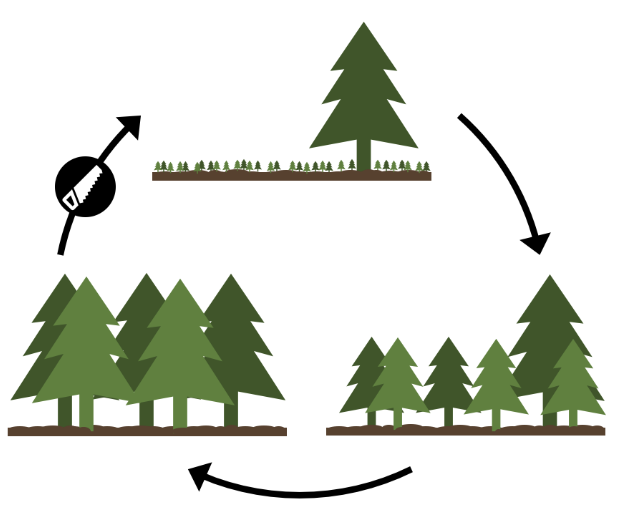
Sustainable forest management is a crucial element in combating climate change, plastic pollution, and other unsolved challenges of the 21st century. A truly optimal forest policy has to balance profit-oriented logging with ecological and societal interests, and should thus be solved as a multi-objective optimization problem. In this paper, we formulate a multi-objective forest management problem where profit, carbon storage, and biodiversity are maximized. Our pioneering work on sustainable forest management explores an entirely new application area for MOEAs with great societal impact.
link / pdf / bibtex
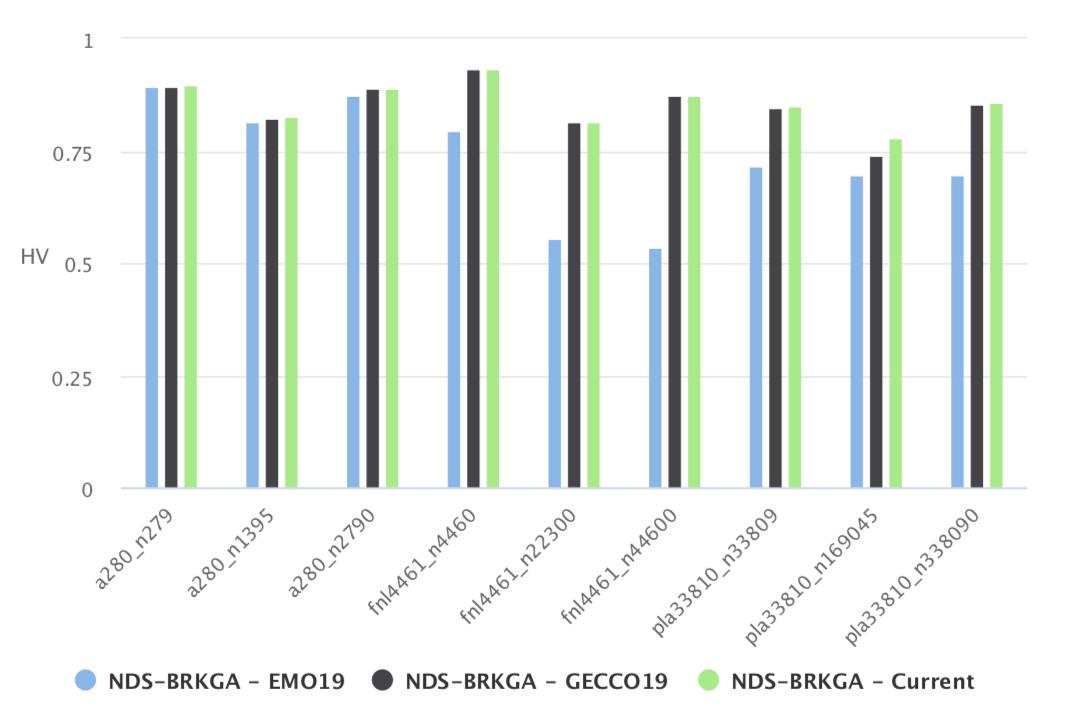
Jonatas Chagas, Julian Blank, Markus Wagner, Marcone Souza, Kalyanmoy Deb
Journal of Heuristics, 2020.
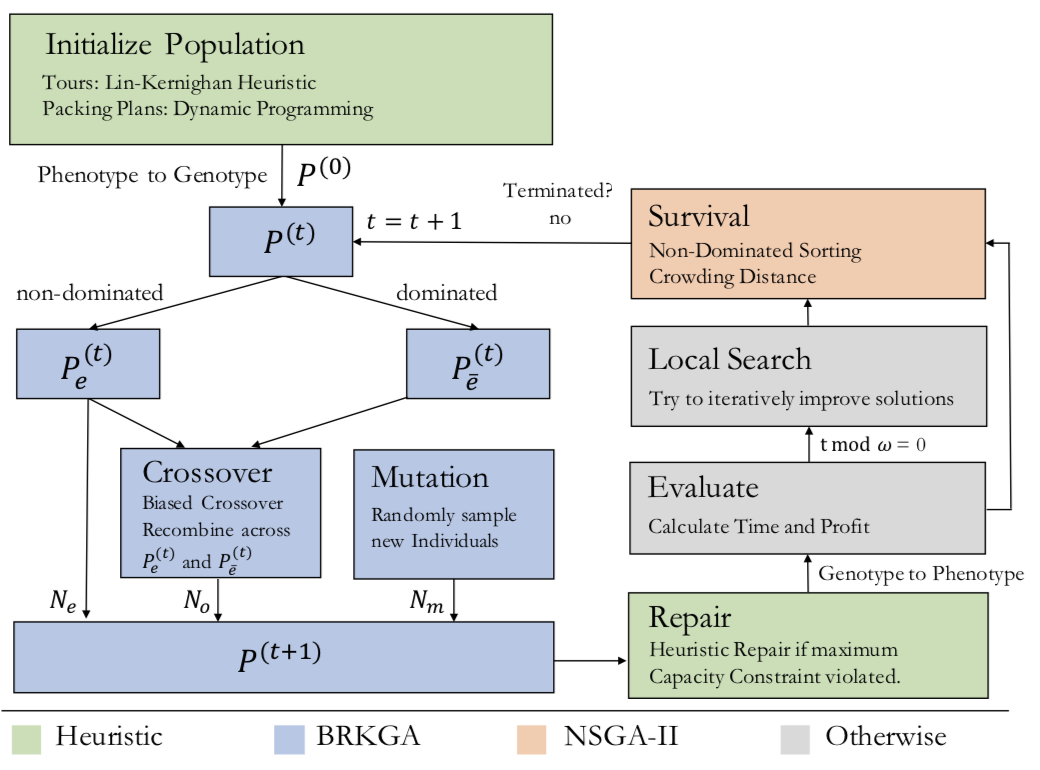
We propose a method to solve a bi-objective variant of the well-studied Traveling Thief Problem (TTP). We address the BI-TTP, a bi-objective version of the TTP, where the goal is to minimize the overall traveling time and to maximize the profit of the collected items. Our proposed method is based on a biased-random key genetic algorithm with customizations addressing problem-specific characteristics. Our method has won first and second places at the BI-TTP competitions at EMO-2019 and GECCO-2019 conferences and, thus, proving its ability to find high-quality solutions consistently.
link / pdf / source code / bibtex
Yash Vesikar, Julian Blank, Kalyanmoy Deb
GECCO, 2020.
We present a formulation of a dynamic bi-objective vessel-to-vessel service ship scheduling problem. In a span of several hours, the service ship must visit as many moving vessels as possible and complete the trip in as small a travel time as possible. We develop a level-wise customized evolutionary algorithm to find multiple trade-off solutions in a generative manner. Compared to a mixed-integer programming (MIP) algorithm, we demonstrate that our customized evolutionary algorithm achieves similar quality schedules in a fraction of the time required by the MIP solver.
link / pdf / poster / slides / bibtex
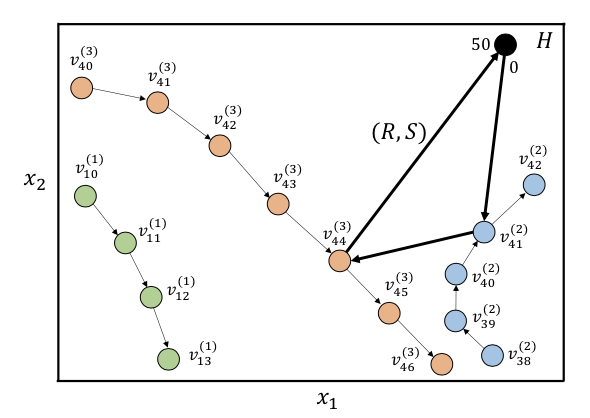
Julian Blank, Kalyanmoy Deb, Proteek Roy
EMO, 2019.
We show the importance of normalization in higher-dimensional objective spaces and provide pseudo-codes which presents a clear description of normalization methods. The results indicate the importance of normalization for the overall algorithm performance and show the effectiveness of the originally proposed NSGA-III’s hyperplane concept in higher-dimensional objective spaces.
link / pdf / slides / source code / bibtex
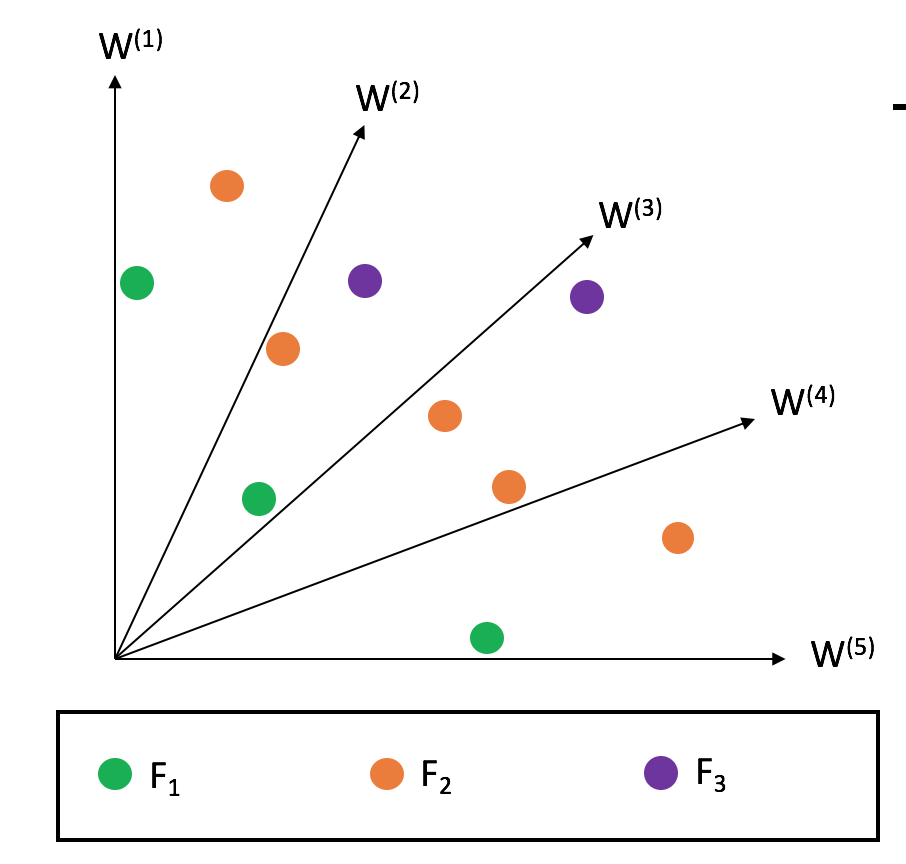
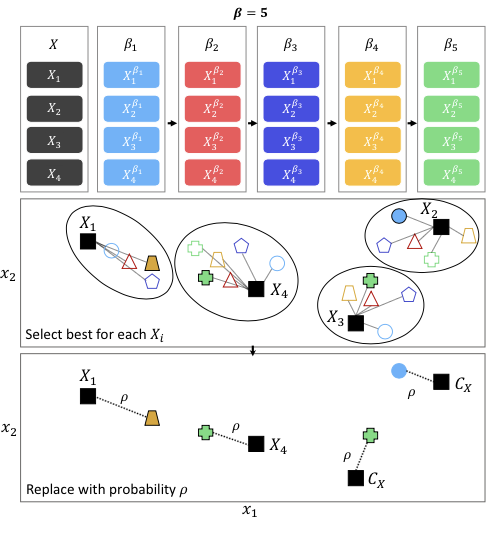
Proteek Roy, Rayan Hussein, Julian Blank, Kalyanmoy Deb
EMO, 2019.
In many practical multi-objective optimization problems, evaluations of objectives and constraints are simulation-based and thus are computationally expensive and time-consuming. We propose a metamodel-based multi-objective evolutionary algorithm that adaptively maintains regions of trust in variable space to make a balance between error uncertainty and progress. The trust regions can grow or shrink in size according to the deviation between metamodel prediction and high-fidelity evaluation.
link / pdf / slides / bibtex
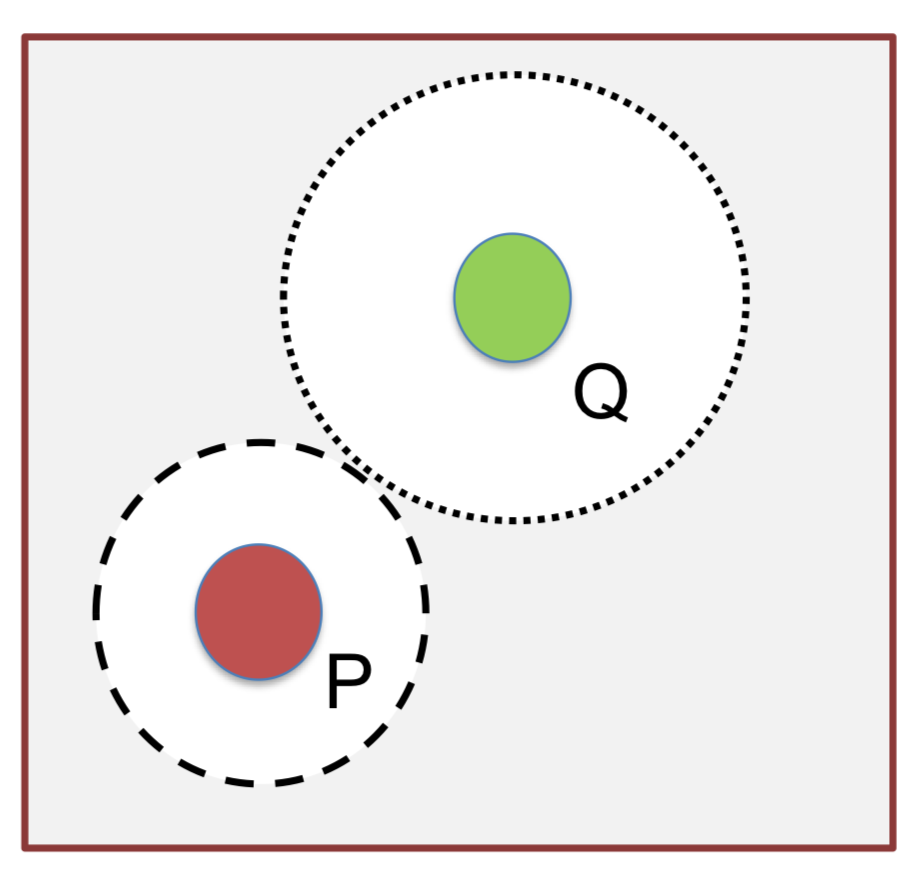
Yash Vesikar, Kalyanmoy Deb, Julian Blank
SSCI, 2018.
The recent advances in evolutionary many-objective optimization (EMOs) have allowed for efficient ways of finding a number of diverse trade-off solutions in three to 15-objective problems. However, in some cases users are interested in finding a part, instead of the entire Pareto-optimal front. Thus, we suggest a reference point based evolutionary many-objective optimization procedure which is an extended version of a R-NSGA-II. The results are encouraging and suggest the use of the concept to other evolutionary many-objective optimization algorithms for further study.
link / pdf / source code / bibtex
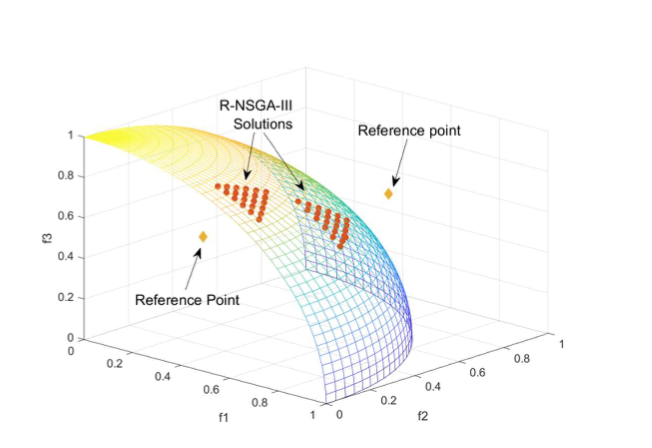
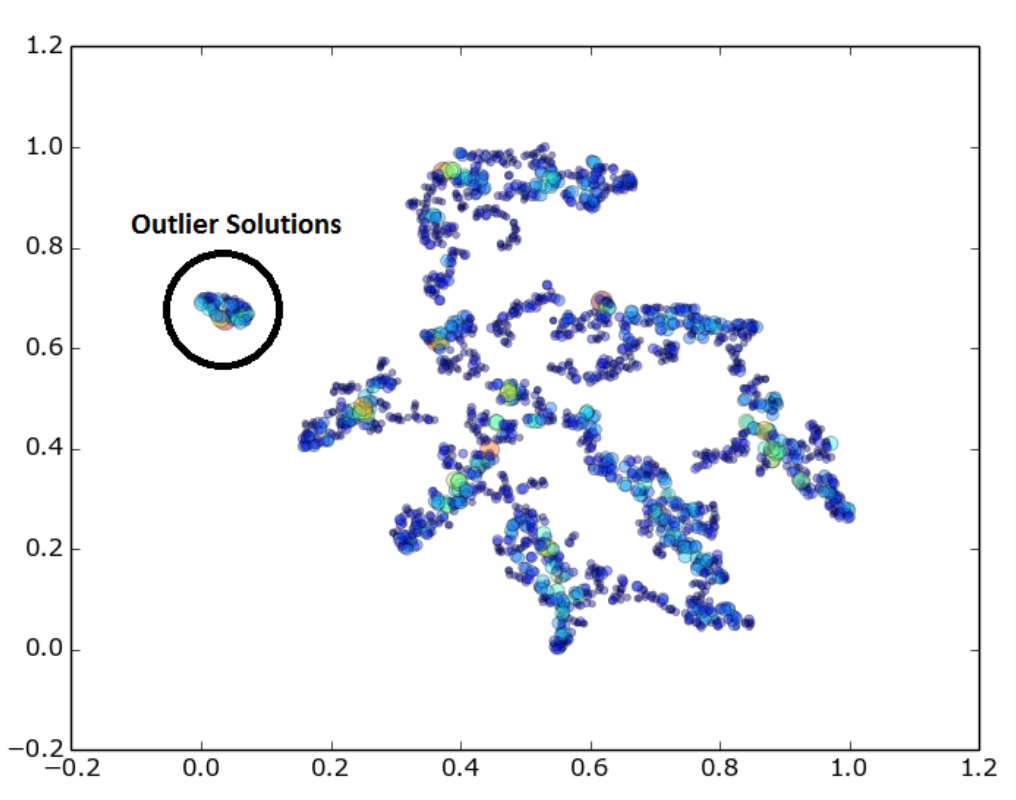
Khaled Talukder, Kalyanmoy Deb, Julian Blank
GECCO, 2018.
We propose an alternative way to visualize high dimensional Pareto-front where the goal is to present the Pareto-front in terms of a decision maker’s perspective. Most of the existing Pareto-from visualization approaches emphasize on the algorithm convergence speed and quality. However, such information is rarely useful in a typical decision making phase. Often, a decision maker is interested in trade-offs, the relative robustness of a solution and how their neighborhood in design and objective space. We present a way to visualize the Pareto-front in high dimension by keeping those criteria in mind. Our approach is in a way similar to that of a scatter plot and, thus, facilitating the decision making process more human centric.
link / pdf / poster / bibtex
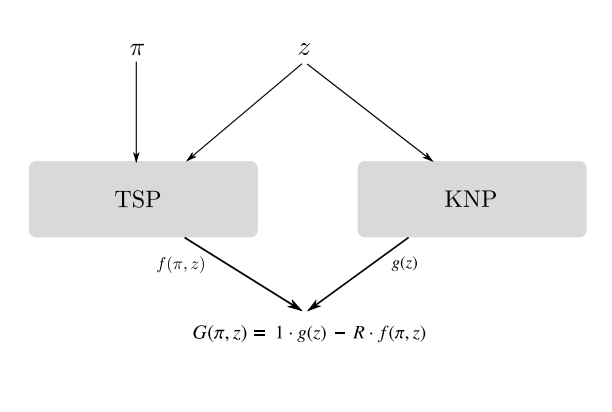
Julian Blank, Kalyanmoy Deb, Sanaz Mostaghim
EMO, 2017.
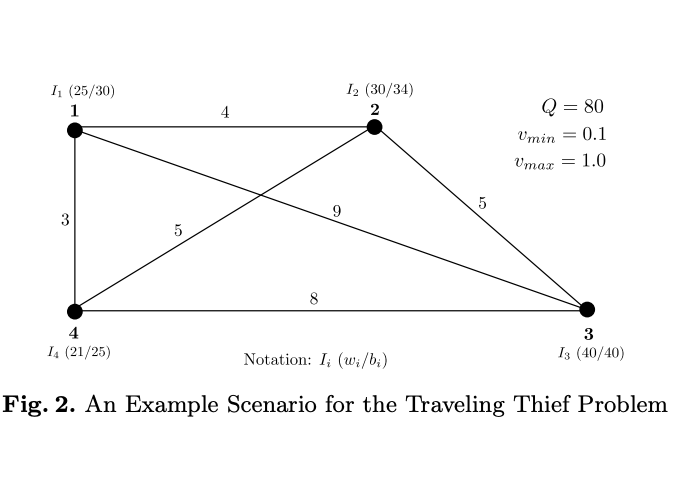
This publication investigates characteristics of and algorithms for the quite new and complex Bi-Objective Traveling Thief Problem. The interdependence of these two components builds an interwoven system where solving one subproblem separately does not solve the overall problem. The first proposed deterministic algorithm picks items on tours calculated by a Traveling Salesman Problem Solver greedily. As an extension, the greedy strategy is substituted by a Knapsack Problem Solver and the resulting Pareto front is locally optimized. These methods serve as a references for the performance of multi-objective evolutionary algorithms. The obtained results provide insights into principles of an exemplary bi-objective interwoven system and new starting points for ongoing research.
link / pdf / bibtex
Julian Blank, Sanaz Mostaghim, Kalyanmoy Deb
Master's thesis, University of Magdeburg.
This thesis presents an in-depth analysis and characteristics of the quite new and complex Traveling Thief Problem (TTP), where the well-known Traveling Salesman Problem and Knapsack Problem interact. Our analyses focus on the interdependence and interwovenness of these components. The obtained results provide insights into characteristics of the single and multi-objective TTP and new starting points for ongoing research.
pdf / bibtex